
But let’s say that you hate it when C-3PO tells you the odds, so you commit to Game 2 because you like the upside potential of $15, and you think the potential loss of $5 is tolerable. After all, Han Solo always beat the odds, right? Well, before you so commit, let me encourage you to look into my crystal ball to show you what the future holds…not just in one future, but many.
C-3PO: “Sir, the possibility of successfully navigating an asteroid field is approximately 3,720 to 1.”
Han Solo: “Never tell me the odds.”
I set up an Analytica model with the following characteristics. A sequence index (Play Sequence) steps from 1 to 1,000. Over this index I will toss two “coins,” one with Probability of Win of 50% (Game 1), and the other (Game 2) with Probability of Win of 45% according to the way I set up the game in my last post. Each Game tosses the coin independently across the Play Sequence, recording the outcome on each step. A Game Reward ($10 for Game 1; $15 for Game 2) is allocated to a win, and a Game Penalty ($0 for Game 1; -$5 for Game 2) is allocated to a loss. Then, I cumulate the net Game Earnings across the Play Sequence to show on what value the cumulative earnings might converge for many repeated games choices. Not only do I play the games over 1000 sequence steps, I also play the sequences across 1000 universes of parallel iterations. From this point forward, I will refer to an “iteration” as the pattern that occurs in one of these parallel universes across the 1000 games it plays in sequence.
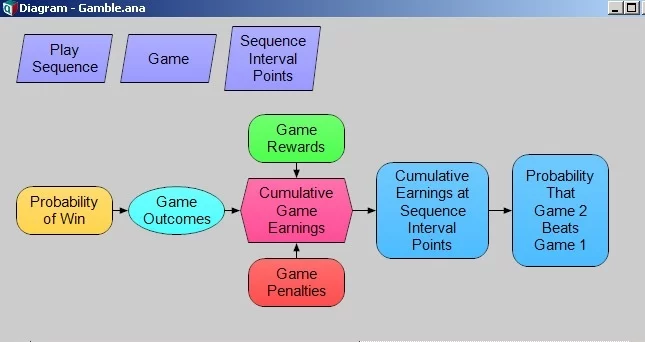
What do we observe? In one iteration, we see you start off accruing net earnings in excess of the higher valued Game 1 across the first 400 or so games; however, your luck turns. You end up regretting not taking Game 1.
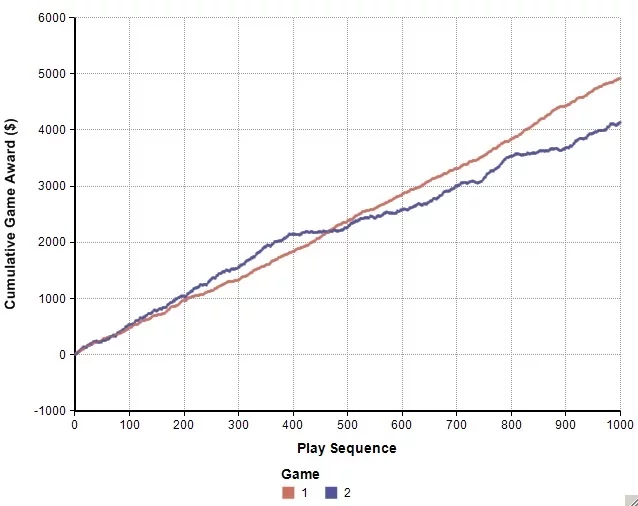
In another iteration, you marginally regret not taking Game 1. You can easily imagine that the outcome could be slightly reversed from this, finding yourself happy that Game 2 just beat out Game 1. Would that outcome prove anything about your skill as a gambler?
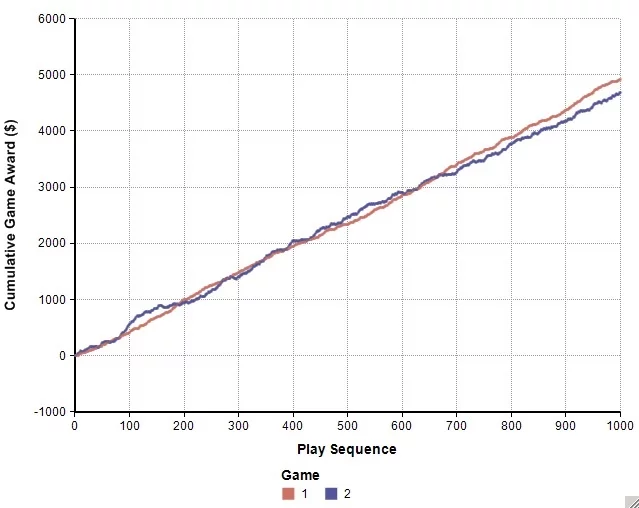
But of course, your luck might turn out much worse. In another iteration, you really regret your bravado.
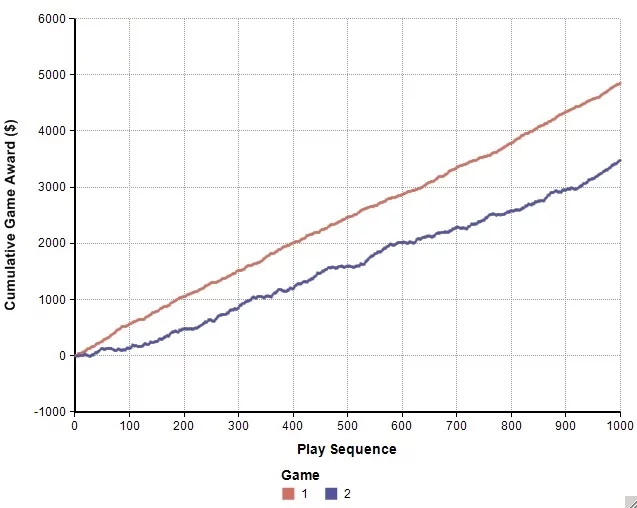
“Of course,” you say, “because the probabilities tell me that I might expect some unfortunate outcomes as well as some beneficial ones. But what overlap might there be over all the iterations at play? Is there some universe in which the odds ever really are in my favor?”
Here’s what we see. For Game 1, the accrued earnings range from ~$4,500 to ~$5,500 by the 1000th step.
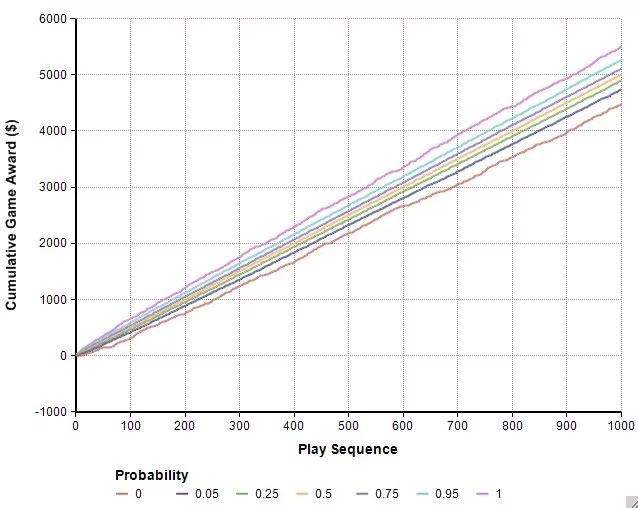
For Game 2, the accrued earnings range from ~$3,000 to ~$5,100. Clearly some overlap potential exists out there.
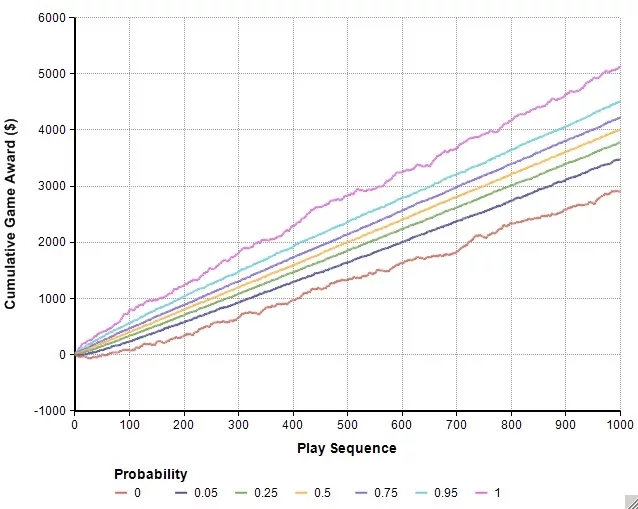
In fact, in the early stages of the game sequences, the potential for overlap appears to be significant, and there seems to be a set of futures where the overlap persists. You might just make that annoying protocol droid wish he had silenced his electronic voice emulator.
But take a second look. That second-from-the-top band for Game 2 converges on the second-from-the-bottom band in Game 1. These are the upper and lower 5th percentile bands of outcome, respectively.
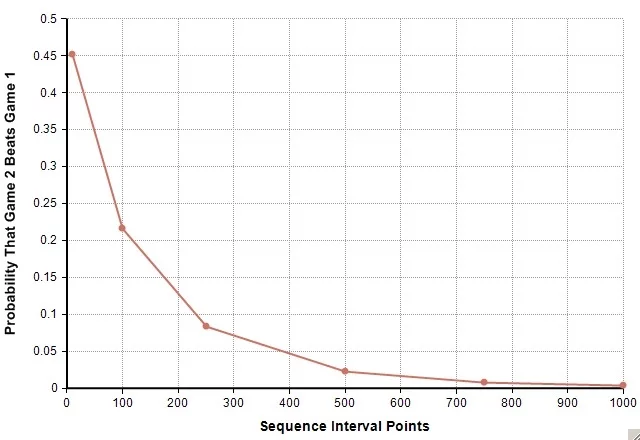
When we count how likely it is that Game 2 ends in winning conditions at various intervals points along the way, the perceived benefit in the higher potential reward of Game 2 decays rapidly. Before you even start, the chance that you could be in a better position by step 1000 for taking Game 2 is around half a percent.
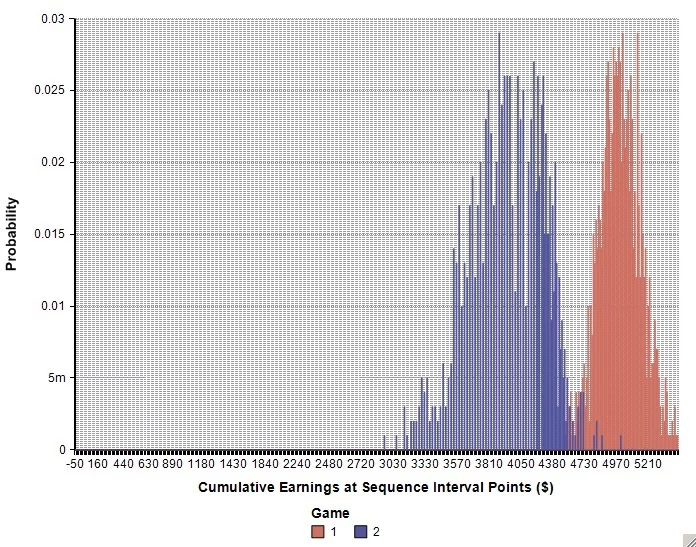
In the model, note that the average earnings by step 1,000 for Game 1 is $5,000 (i.e., 1000*EV1) and that the earnings for Game 2 is $4,000 (i.e., 1000*EV2). It’s as if the imputed EV of each game inexorably accumulated over time…a very long time and over many universes.
So it is in the fantasy of Hollywood that the mere mention of long odds ensures the protagonist’s success. Unfortunately, life doesn’t always conform to that fantasy. Over a long time and many repeated occasions to play risky games, especially those that afford little opportunity to adjust our position or mitigate our exposure, EV tells us that our potential for regret increases for having chosen the lesser valued of the two games. Depending on the relative size of the EVs between the two choices, that potential for regret can occur rapidly as the inherent outcome signal implied by the EV begins to overwhelm the potential short-term lucky outcomes in the random noise of the game.
So how can you know when you will be lucky? You can’t. The odds based on short-term observations of good luck will not long be in your favor. Your fate will likely regress to the mean.




