Monte Carlo simulation software

Monte Carlo simulation & risk analysis: what you can learn & how you can benefit
Ready for some Monte Carlo? No, not the solitaire card game, nor even a trip to the grand casino in Monaco — but rather a Monte Carlo simulation, a way to understand and manage risk and uncertainty using probabilities.
While the Monte Carlo simulation might have its origin in particle physics, it is now widely used by businesses and decision-makers of all types to analyze risk and uncertainty. Monte Carlo simulations are used to estimate return on investment, cope with risks from pathogens or cyberattacks, optimize inventory levels, plan product launches, and much more.
The mathematical algorithms underlying Monte Carlo methods may seem complex, but nowadays a range of software tools — like Analytica — handle all these complexities for you. They enable analysts and decision-makers to use these powerful techniques seamlessly and efficiently via intuitive use interfaces without requiring any special expertise.
Let’s dig a bit deeper into Monte Carlo simulation, how it works, what advantages it offers, and how it helps companies thrive amid risk and uncertainty.
Monte Carlo simulation: A definition
Quantitative models invariably rely on uncertain assumptions; the world, life and business unfold in unpredictable ways. Price changes, project delays, cost overruns and unexpected opportunities are all within the realm of possibility. How can decision-makers fully understand their probabilities and effects?
That’s where Monte Carlo simulation comes in. This method uses repeated random sampling to assign a random value to each uncertain input between minimum and maximum values. Then, the simulation can be run hundreds or thousands of times over to produce a probability distribution over the results in question — return on investment, net present value, or whatever you care about.
With a full distribution over possible futures, decision-makers can envision the full range of outcomes, and develop robust and resilient decisions.
A quick history

Let’s take a step back to the origins of the modern Monte Carlo method to see how it works.
The basic idea first popped into the head of Polish-American mathematician and nuclear physicist Stanislaw Ulam when he was playing solitaire in 1946. Ulam was working on nuclear fission at Los Alamos as part of the Manhattan Project.
According to the Los Alamos National Laboratory journal, Ulam said:
“The first thoughts and attempts I made to practice [the Monte Carlo method] were suggested by a question that occurred to me in 1946 as I was convalescing from an illness and playing solitaires. The question was what are the chances that a solitaire laid out with 52 cards will come out successfully? After spending a lot of time trying to estimate them … I wondered whether a more practical method than “abstract thinking” might not be to lay it out [100] times and simply observe and count the number of successful plays.”
In his research, Ulam was exploring the behavior of neutrons in the nuclear fission chain reaction. Ulam and his partner, John von Neumann, had a set of variables (e.g., velocity, time, direction of movement, path length, and type of collision), many of which were uncertain.
They then began a set of random experiments using early computer technology, assigning a random value to as many as seven unknown variables to produce a probability distribution. Because their work was classified, it had to be given a code name. As it happened, Ulam had an uncle that would frequent the Monte Carlo casino — the rest is history.
How a Monte Carlo simulation works
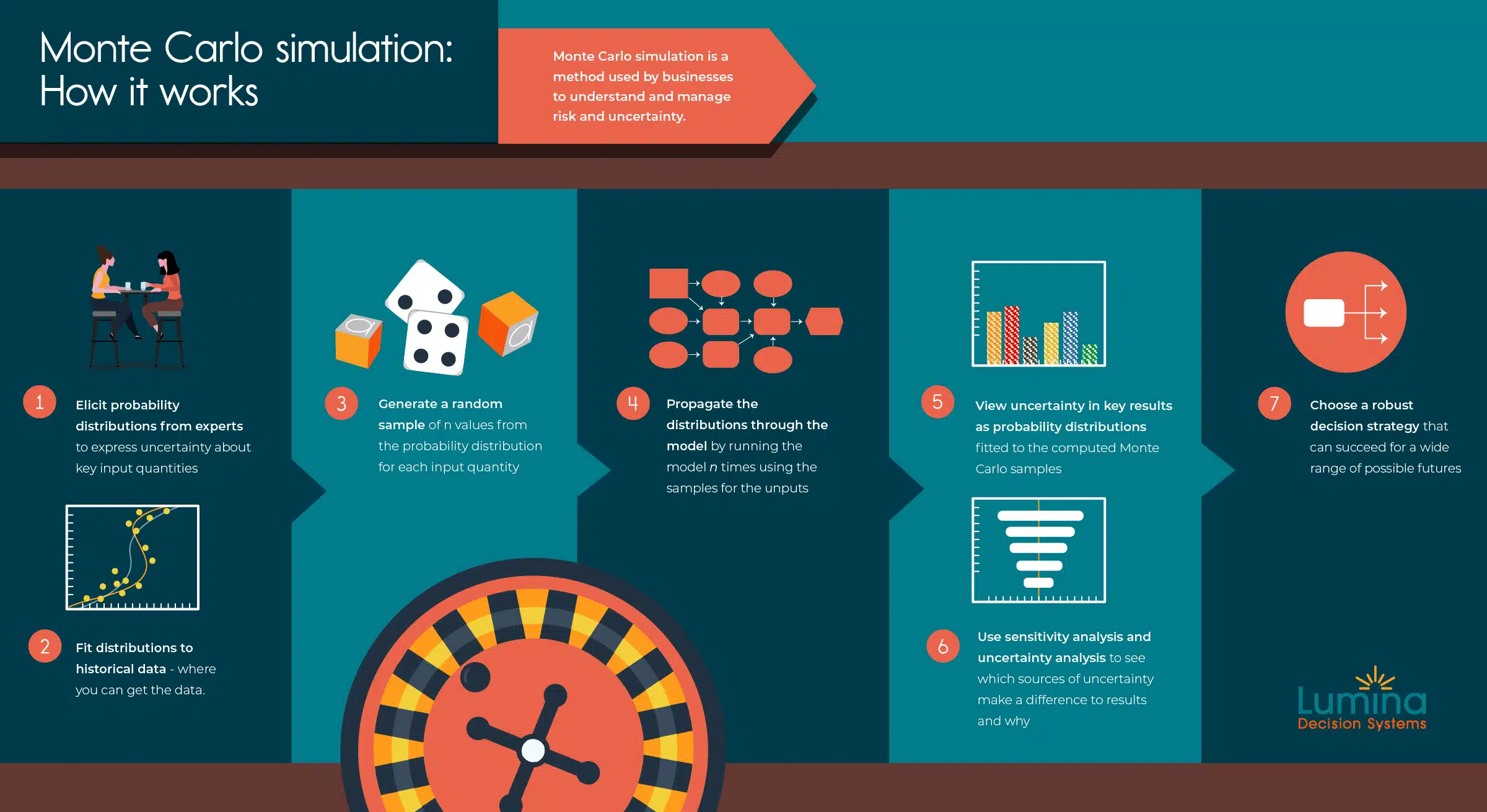
In standard Monte Carlo simulation, you specify the uncertainty in each input as a probability distribution — uniform, normal, Bernoulli, or other distribution. You can fit distributions to data from past values of each quantity, or obtain them from subject matter experts as a way to express their uncertain knowledge about the quantity. Sometimes it is a combination of empirical data and expert judgment.
The software samples a random value from each input distribution and runs the model using those values. After repeating the process a number of times (typically 100 to 10,000), the simulation estimates probability distributions for the uncertain outputs of the model using the random sample of output values. A larger number of samples takes longer to compute for a complex model but enables a more accurate estimate of the resulting distributions, including their mean (expected value), standard deviation, median, or percentiles.
That does not mean, however, that the Monte Carlo simulations cannot be run efficiently and speedily at scale. A common misconception is that the computational effort is combinatorial (exponential) in the number of uncertain inputs — which would seemingly make it impractical for large models. This is true for simple discrete probability tree (or decision tree) methods. But, in fact, the great advantage of Monte Carlo is that the computation effort scales linearly with the number of uncertain inputs: I.e., computation time is proportional to the number of uncertain quantities.
The required sample size is determined by the degree of precision of the output distributions you care about. Suppose you are interested in estimating percentiles of a cumulative distribution; there’s no need to increase the sample size just because you have more uncertain inputs. For most models, a few hundred up to a thousand runs are sufficient. You only need a larger sample if you want high precision in your resulting distributions and a smooth-looking density function. Given the inherent uncertainty, higher precision is usually an aesthetic preference rather than a functional need.
What are the advantages of Monte Carlo simulations?
Performing a Monte Carlo simulation offers a number of advantages over deterministic calculations across an array of decision-making applications.
The topline advantage of a Monte Carlo simulation is to faithfully address uncertainty in a quantitative model. The most common approach to uncertainty is to make like the ostrich and stick one’s head in the sand, treating uncertainty as if it does not exist. You might use what you think is the “most likely” or average value of each uncertain variable. This does not, however, guarantee that you will get the most likely or average value in the model results.
This deficiency can be seen in the Flaw of Averages — pardon us, the Law of Averages. This axiom posits that if you repeat an unpredictable experiment enough times, you’ll arrive at the average outcome, with results balanced on either side of deviation.
However, consider a drunk trying to walk down the middle of a busy two-lane highway. If you assume he stays at his average position on the centerline, he’ll survive. In reality, he staggers left and right. The state of the drunk in his average position is alive but his average state is dead.
Another common flaw in our intuition about probability is the Gambler’s Fallacy that after a run of one outcome another outcome is “due” — a famous case occurred in 1913 at the Monte Carlo Casino. On the night of August 18, the roulette ball fell on black 26 straight times. Some gamblers were run broke during this stretch, continually betting on red and against black in a “common-sense” approach that the ball would average out to black soon enough. The ball would eventually touch red again, but it was too late for many.
Monte Carlo simulation can provide a reliable inoculation against the natural biases, confusion, and, most importantly, wishful thinking that we often bring to dealing with uncertainty.
Comparing Monte Carlo analysis to other methods

An understanding of the advantages of a Monte Carlo simulation can also be elucidated by comparing it to other methods of treating uncertainty.
- There are analytic methods for propagating uncertainty — as opposed to numerical — through a model based on mathematical approximations. A common approach is “error propagation,” which lets you estimate the relative error (i.e., the ratio of standard deviation to mean) based on the relative error of inputs. It works well for simple, smooth models and small relative errors. But, it takes a considerable amount of algebra to analyze each formula, and the results are only approximate. It doesn’t work well for models with steps and other non-smooth functions, or when the uncertainties are large.
- Another option is to use probability trees, for which you approximate each uncertain quantity by a small number of discrete outcomes, such as low, median, and high values, each with an assigned probability. You can then represent your model as a tree where each uncertain quantity branches out with these outcomes. You estimate the value of the result at each endpoint. This method is often combined with decision variables, each also represented as a small number of options. The result is a decision tree. These are intuitive and useful for models with a small number of uncertainties and decisions. But, the number of endpoint outcomes increases exponentially with the number of variables. For example, with four uncertainties and three decisions, you end up with 2,187 endpoints. So, it rapidly becomes intractable for substantial problems with many uncertainties.
- With scenario analysis, you define a scenario by selecting a particular value for each uncertain quantity and decision and compute the corresponding result. If you keep the number of scenarios small, typically three to five, the results are intuitive. The problem is that these results tell you nothing about the relative probability of each scenario. And, you have no sense of whether you have good coverage of the parameter space, or of the interactions among the variables.
Where do you get the input probability distributions?
Would-be users of Monte Carlo simulation often wonder about how to obtain probability distributions to express the uncertainty in each uncertain input or parameter. Often, they look for data that seems relevant (sometimes historical data) from which to estimate these distributions.
Say that we’re trying to estimate next year’s sales of a software product. It’s certainly helpful to look at sales in past years. If you have 10 years of past sales, you could estimate the mean and standard deviation and fit a normal distribution. Better yet, you can see a trend over the last 10 years. You could also use a regression, or time-series analysis, to fit a trend line, along with statistical methods to estimate the uncertainty based on the quality of the fit to past data.
But, fitting a trend line assumes that you expect next year’s sales to be a simple extrapolation of last year. It’s likely, however, you know something that can’t be seen in past sales data. Perhaps you expect a major competitor to enter this market next year. Or, the product manager is planning a big improvement in your product or a price drop. There is no simple formula to adjust your forecast. So you must rely on expert judgment — perhaps your own analysis or you might consult an expert in the market for this kind of software.
Even in the rare case that you have a lot of relevant historical data, you must still make a judgment that the future will be similar to the past if you want to simply follow the historical trend. More often you have little or no data that is directly relevant, but you have some expert knowledge to help in making these judgments. Too often modelers jump to using a single “best estimate” for each assumption. They worry that using expert judgment will make the results “subjective.” The reality is that there is always a need for judgment since there is never enough data — especially since we just can’t get data from the future, which is usually what we are modeling. It’s better to be explicit, and use a careful process to estimate and express the expert judgment and its associated uncertainties than to try to hide the inevitable judgments under the carpet of “fake certainty.”
What you need to perform a Monte Carlo simulation

Coding an efficient, robust, reliable Monte Carlo simulation from scratch is a challenging project. Fortunately, there are several software packages that make it easy by including Monte Carlo methods as part of a quantitative modeling tool.
With a Monte Carlo package, the first step is to define each uncertain input variable as a probability distribution, whether fitted to historical data or expert judgment, or some combination. You may choose a standard parametric distribution, such as the Normal, uniform, triangular, beta, and so on. Or you may fit a custom distribution to selected points from the cumulative distribution, such as 10th, 50th, and 90th percentiles, along with minimum and maximum.
Then you specify the sample size for your Monte Carlo simulation, perhaps a small one of 100 to 400 for initial explorations. Then for the final results, you might choose a larger sample, perhaps 2000 to 10,000, where you want a smooth and accurate representation of the computed distribution. Then you run the simulation and view the distributions fitted to the resulting samples.
If your models are in a spreadsheet, you can use a variety of add-in packages for spreadsheets to do Monte Carlo simulation. Retrofit packages for Microsoft Excel include @Risk from Palisade, Oracle Crystal Ball, Frontline Analytic Solver, and the SIPMath package. However, it is often more convenient and faster to use a quantitative modeling environment, like Analytica, which integrates Monte Carlo simulation into its original design. This approach offers major advantages in terms of ease of use and speed of computation.
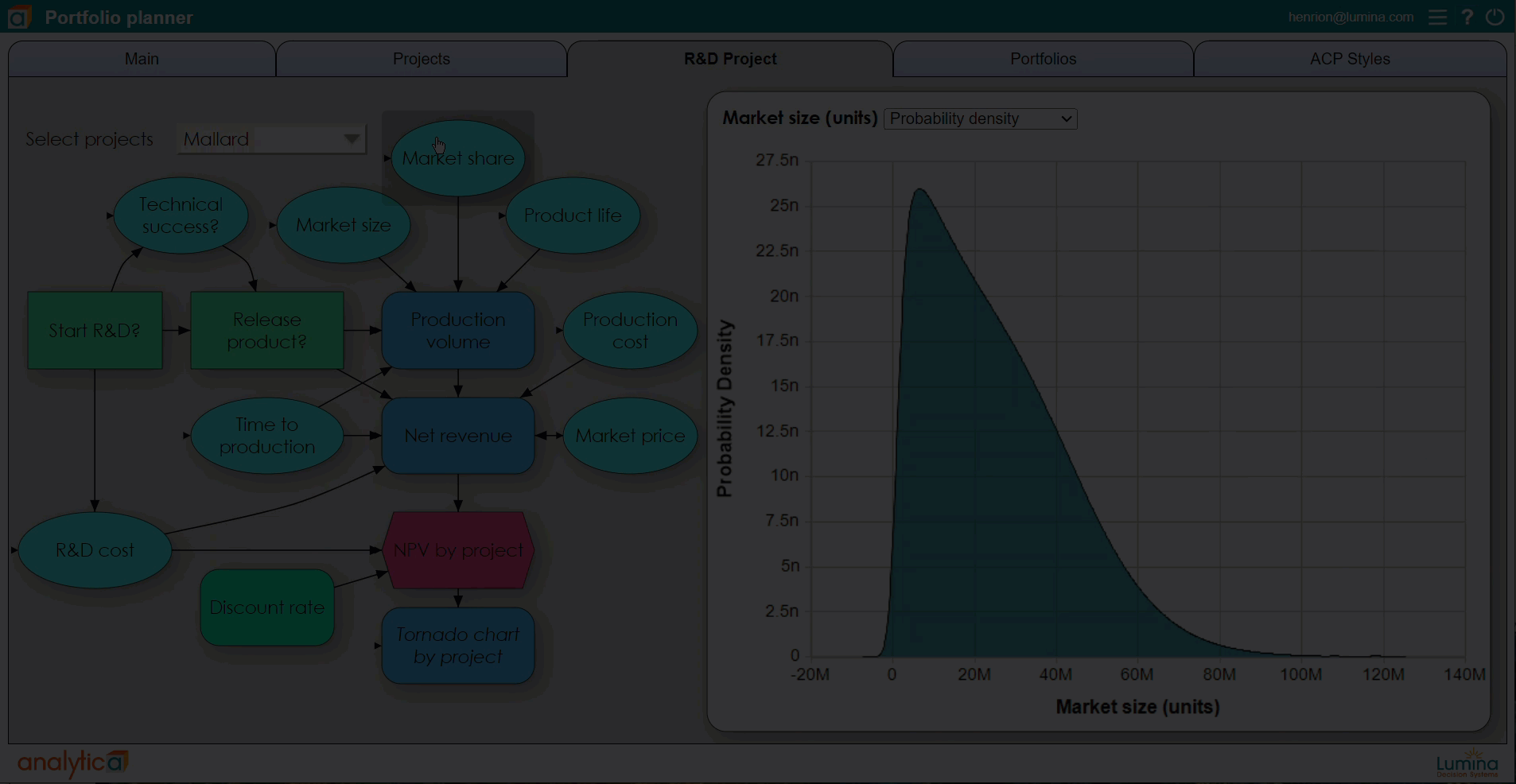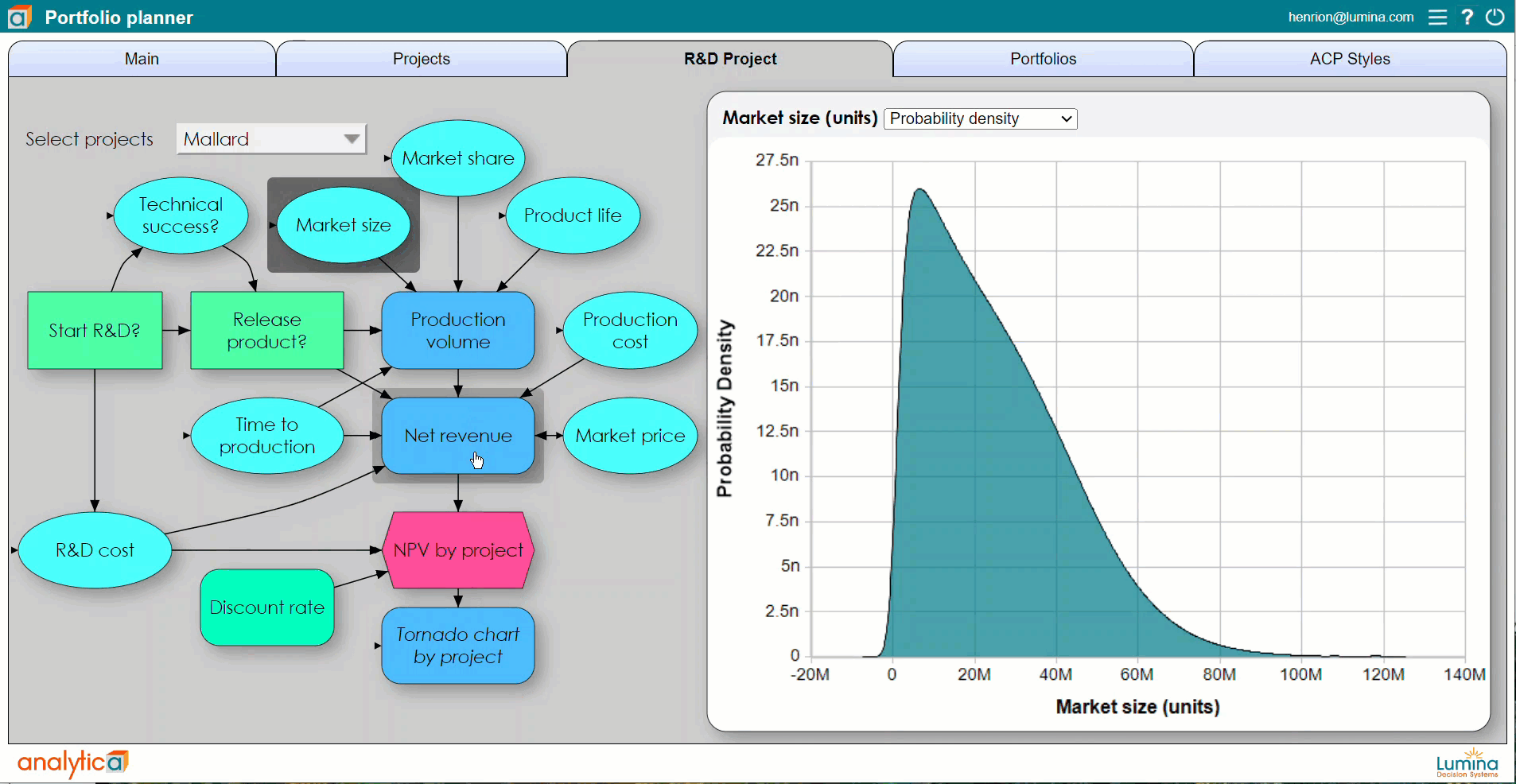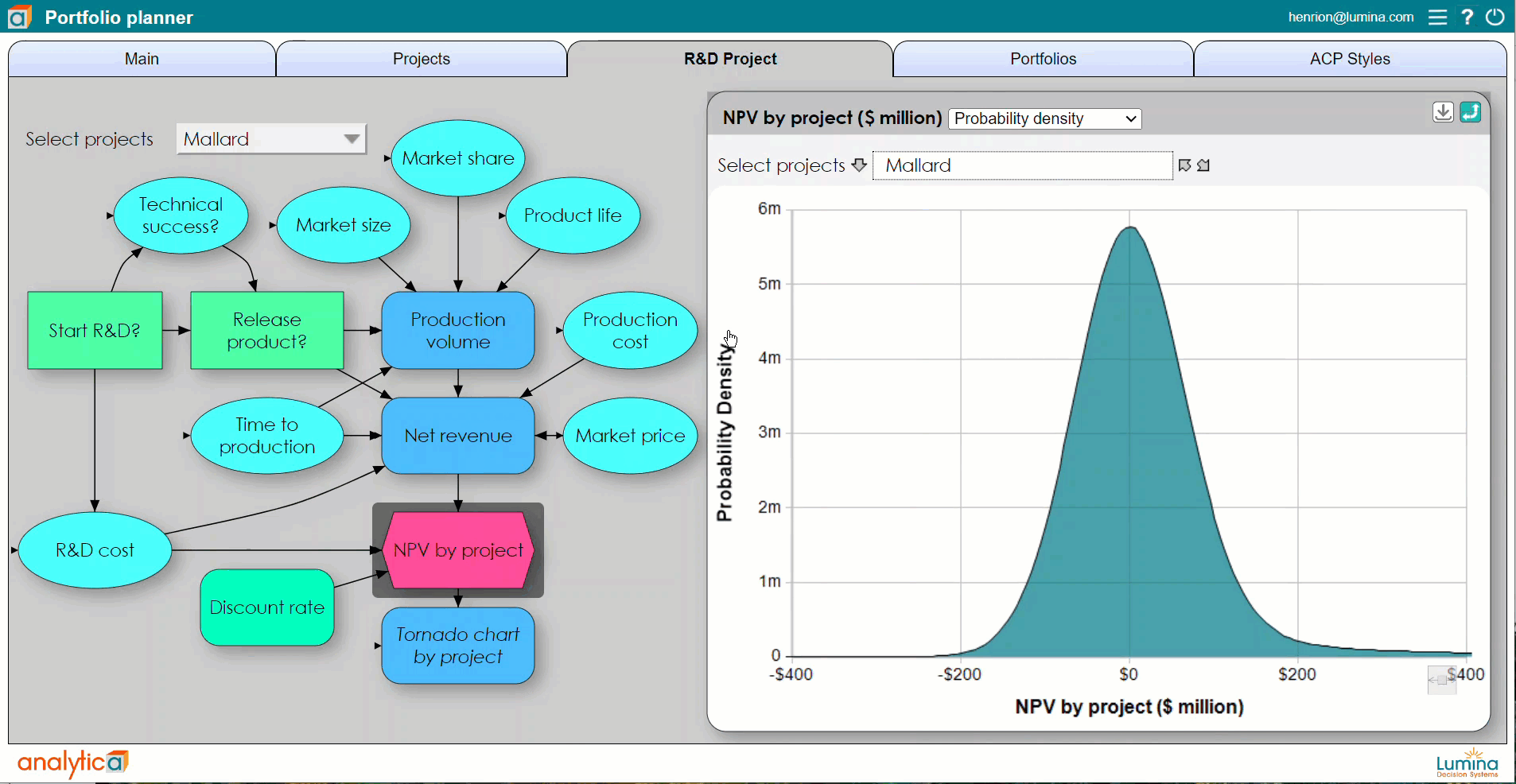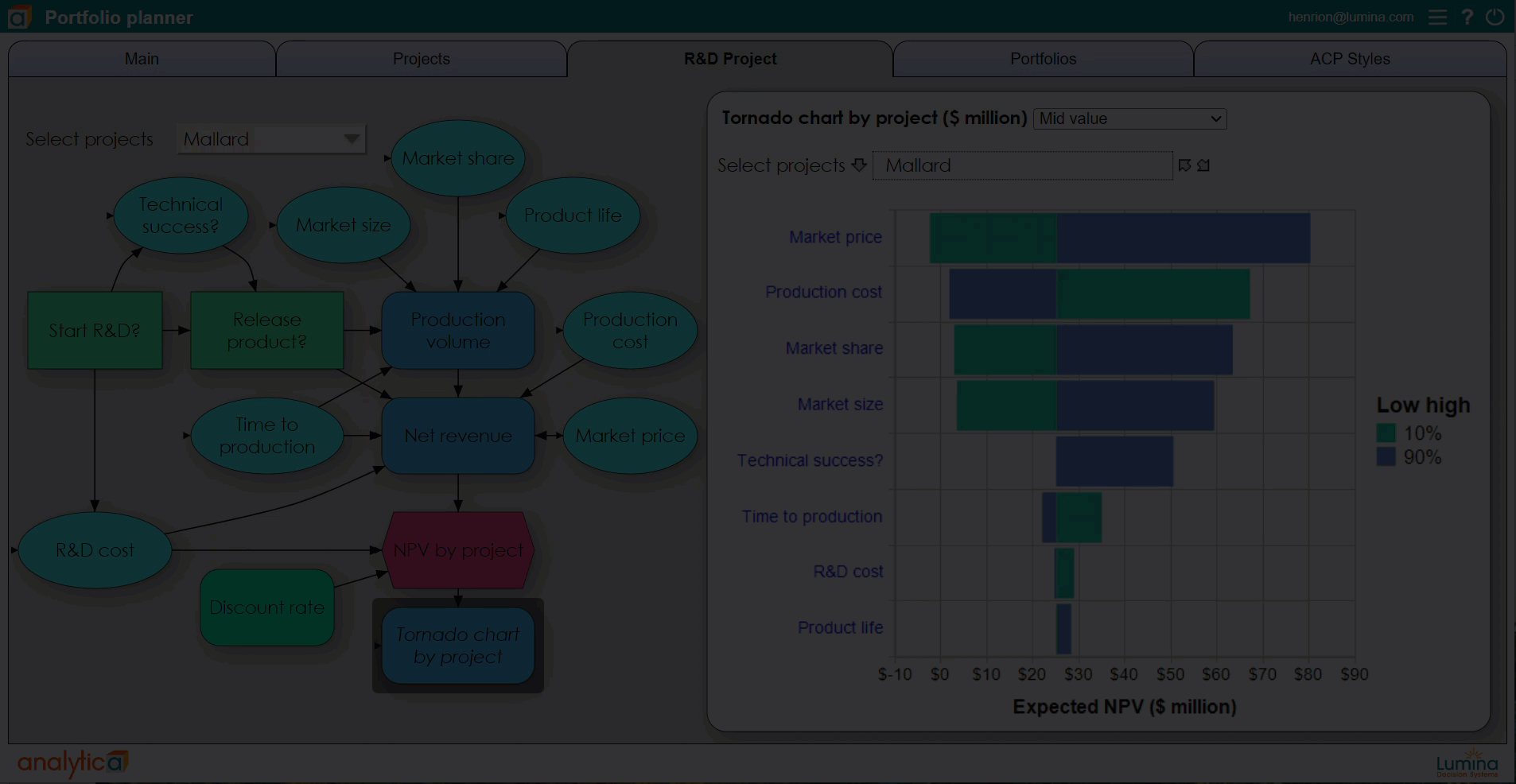
Using Analytica, you can define any variable, or any cell in an array, as a discrete or continuous distribution. You can view the probability distribution for any resulting variable as a set of probability bands (selected percentiles), as a probability density function, cumulative distribution function, or even view the underlying random sample. A particular advantage is that Analytica’s simulation tools are fully integrated with its Intelligent Arrays. This makes it vastly easier to define and analyze multivariate variables with serial correlation such as sales or interest rates over time, and cross-dependency across multiple regions and products.